Lecture 3: Summary

• Regularization
• Stochastic Gradient Descent
• Momentum, AdaGrad, Adam
• Learning rate schedules

Regularization

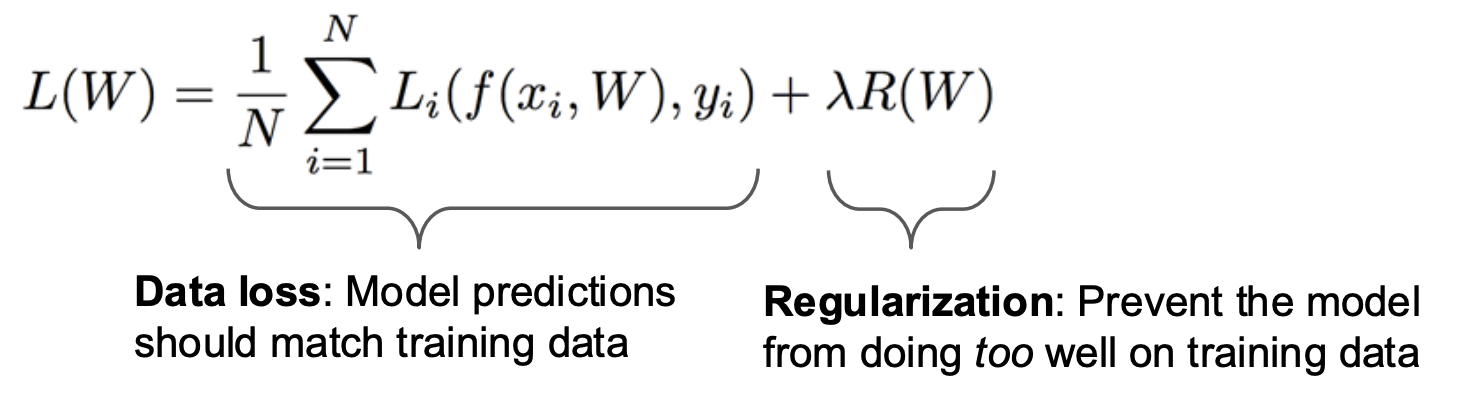
Occam의 면도날(Occam's Razor)이라는 간단성의 법칙이 있다.
여러개의 가설이 존재할 때, 가장 간단한 것이 최선이라는 의미이다.

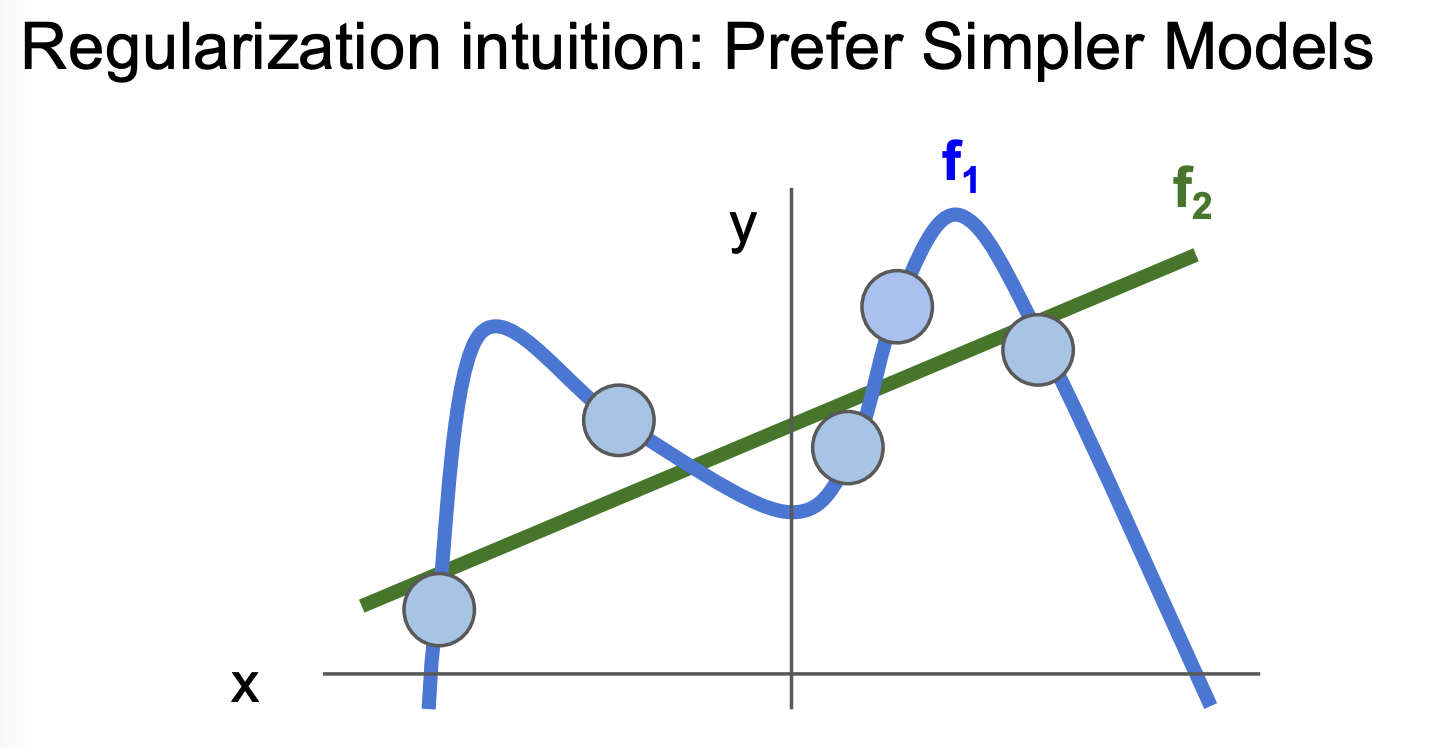
예를 들어, 위 5개의 데이터 포인트를 설명하는 두 함수 f1과 f2 중에 어느 것이 더 좋은 설명 함수일까?
어떤 다음 포인트를 더 잘 예측할 수 있을까?

f1은 현재까지의 데이터를 100% 완벽하게 설명하지만, f2는 어느 하나도 정확히 맞추지 않는다.
하지만 우리는 f2가 다음 번 데이터를 더 근접하게 예측할 것이라고 어렵지 않게 상상한다.

이처럼 과도하게 설명되는 오버피팅을 막기 위해 정규화 메소드를 사용한다.

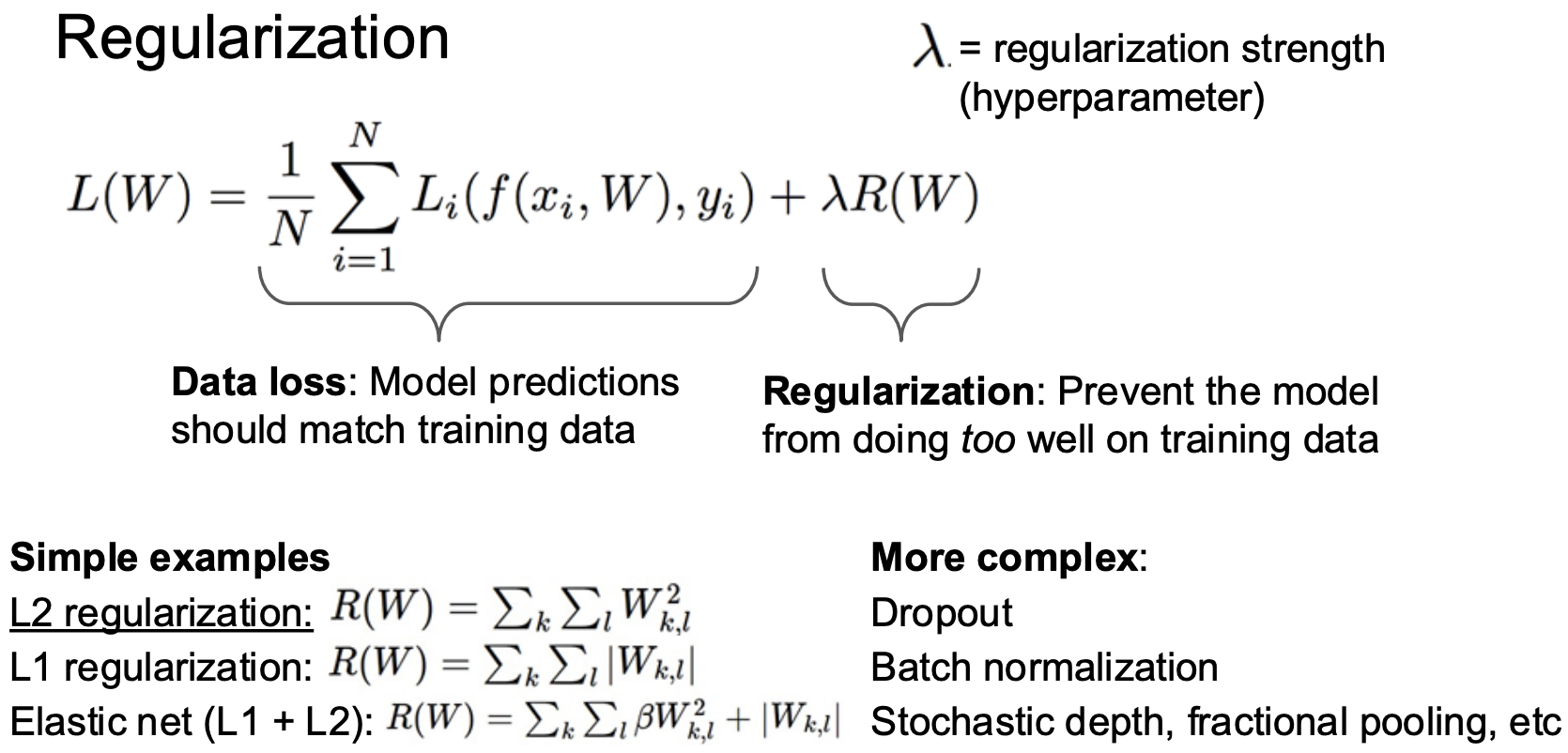
간단한 예시를 들어보자,

보이듯이, w1과 w2는 모두 동일한 로스를 만들어 내는 가중치이다.
그렇다면, 이 둘 중에 무엇이 더 좋은 가중치 파라미터일까?

L2 metric을 이용해 예시를 들어보면, w1과 w2의 R(W)는 각각 1, 1/4 이다.
이처럼 정규화는 가중치 요소들이 더 많이 퍼져있는 w2를 선택하도록 작동한다.

따라서 이러한 로스항에서 w2가 더 큰 로스를 갖게 된다.

Gradient Descent

문제 정의: 결국 로스가 낮게 나오는 파라미터가 무엇인지가 문제의 핵심이다.
가장 일반적인 baseline으로 random search를 생각해볼 수 있지만, 시간은 무한하지 않기 때문에 우리는 더 나은 탐색 방법을 생각해봐야 한다.

Follow the slope

아래는 함수 $L(x)=x^4-3x^2-x$의 그래프이다. 함수 $L(x)$는 우리가 최솟값을 찾아야 하는 loss이다. $L(x)$의 최솟값을 구하는 가장 좋은 방법은 도함수가 0이되는 지점을 찾는 것이다. 지금은 그럴 수 있다. 하지만, 파라미터가 1000개라면 어떨까? RSS의 최소제곱합을 미분하여 0이 되는 지점들을 구하려면, 미지수가 1000개인 연립 2차 방정식을 풀어서 1000개의 해를 찾아야 한다. 이처럼 파라미터의 증가에 따른 기하급수적인 계산량을 감당할 수 없다.

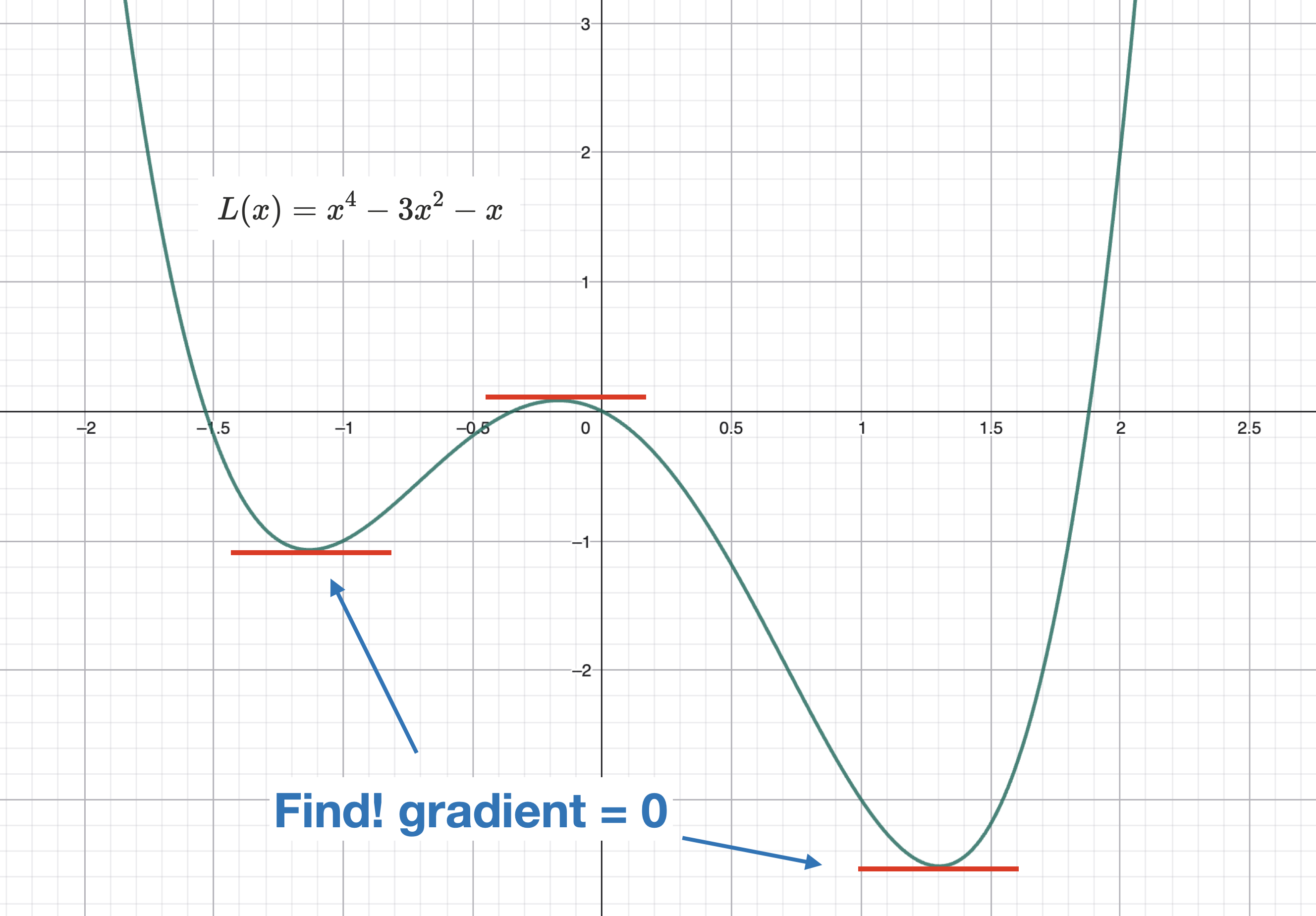
따라서, 방정식을 푸는 방식으로 접근할 수는 없다.
미분방정식을 풀 수 없다면, 대입법을 사용할 수 밖에 없다.
조금씩 숫자를 바꿔서 대입해가며, 로스값을 추적한다. 로스가 감소하는 방향성을 따라 조금씩 더듬더듬 찾아가는 것이다. 그러다 보면 아래 그림처럼 전역 최소(Best)가 아닌, 로컬에서만 최소인 지점으로 수렴하는 문제가 발생할 수도 있다. 이는 바로 뒤에서 다룬다.

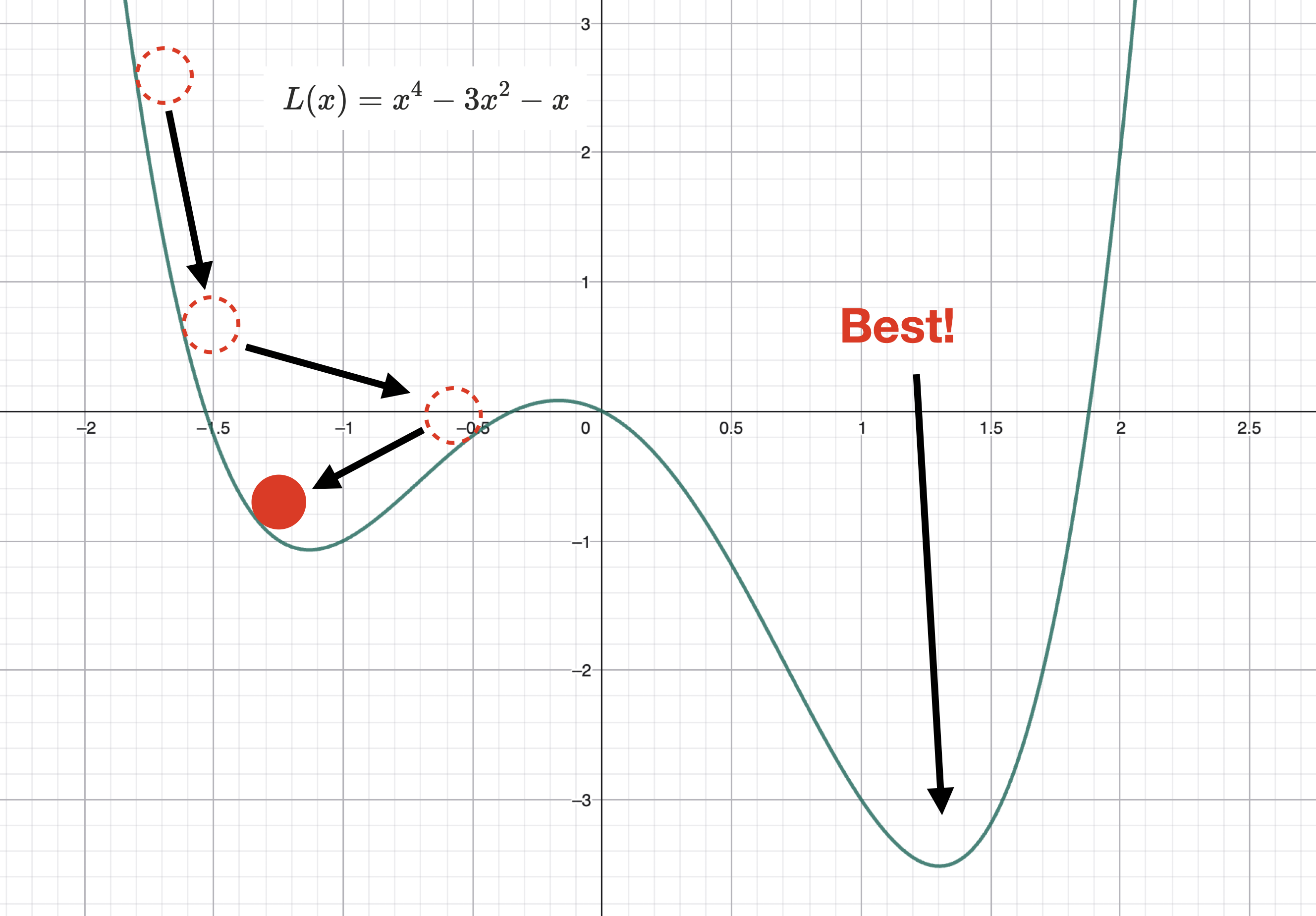
로스가 감소하는 방향성을 구하기 위해서는 미분을 통해 기울기를 구해야 한다.
지난시간에 배운 한 softmax loss를 예시로 들어보자,

여기서 우리가 구하고싶은 것은 파라미터 W에 대한 로스의 그라디언트 값이다.
이러한 그라디언트 미분 연습은 Calculating Gradient에서 충분한 연습을 해보았으므로, 넘어간다. 계산시 스칼라, 벡터, 매트릭스, 텐서 등 차원에 유의한다. 직관적 이해를 위해 수치 미분을 이용해 계산하는 예시를 남긴다. 수학적 기초는 Calculus II 학습이 필요하다.

수치 미분(numerical gradient)

미분계수의 정의는 다음과 같다.

미분소 h 대신 아주 작은 값을 사용해서 미분계수를 근사할 수 있다. 위 함수의 예시를 들어보자.
$x=-2$ 일 때, $L(-2+0.01)=\mathbf{5.792}...\approx L(-2)+L^{\prime }(-2)\times 0.01=6-21\times 0.01=\mathbf{5.79}$
$x=-1$ 일 때, $L(-1+0.01)=\mathbf{-}\mathbf{0.989}...\approx L(-1)+L^{\prime }(-1)\times 0.01=-1+1\times 0.01=\mathbf{-}\mathbf{0.99}$

마찬가지로 가중치 W에 대해서도 각 파라미터에 돌아가며 충분히 작은 값을 더하여 softmax loss $L$의 그라디언트인 $\mathrm{\nabla }L$의 근사치를 구할 수 있다.
하지만, 이는 부정확하고 느리기 때문에 gradient check용으로 주로 쓰인다.

이제 GD에서 생각해봐야 할 문제는 두 가지이다.
어떻게 파라미터를 업데이트 할 것인지와 얼마나 빠르게 업데이트할 것인지이다. 이를 통해 앞서 언급한 로컬 최소에 빠지는 문제를 해결하는 것도 볼 수 있다.

Gradient Descent

# 기본 GD
while True:
    weights_grad = eval_grad(loss_ftn, data, weights) # 평균 그라디언트 계산
    weights += - step_size * weights_grad # 가중치 업데이트

GD는 이런식으로 N개의 모든 데이터의 로스를 평균내서 전체 로스를 구한다. 이것은 N이 아주 클 때, 너무 시간이 오래걸린다.

Stochastic Gradient Descent (SGD)

# 미니배치 SGD
while True:
    data_batch = sample_training_data(data, 256) # 랜덤으로 미니배치 샘플링
    weights_grad = eval_grad(loss_ftn, data_batch, weights) # 그라디언트 기댓값 계산
    weights += - step_size * weights_grad

생각해보면, 굳이 전체 데이터를 볼 필요가 없다. 충분히 랜덤한 표집을 수없이 할 수 있다면, 그것은 통계적으로 모집단에 대한 유의미한 대푯값이 될 수 있기 때문이다.

SGD + Momentum

RMSProp

Adam

AdamW

옵티마이제이션 아이디어
2^n 슬라이싱 기반 n회최적화 이후 추가 최적화.

Scheduler